Clustering Coefficient Of A Tree

Oktober 27, 2021 Posting Komentar

In this respect the clustering coefficient of a graph is widely used in network analysis. Each observation starts in its own cluster and pairs of clusters are merged as one moves up.

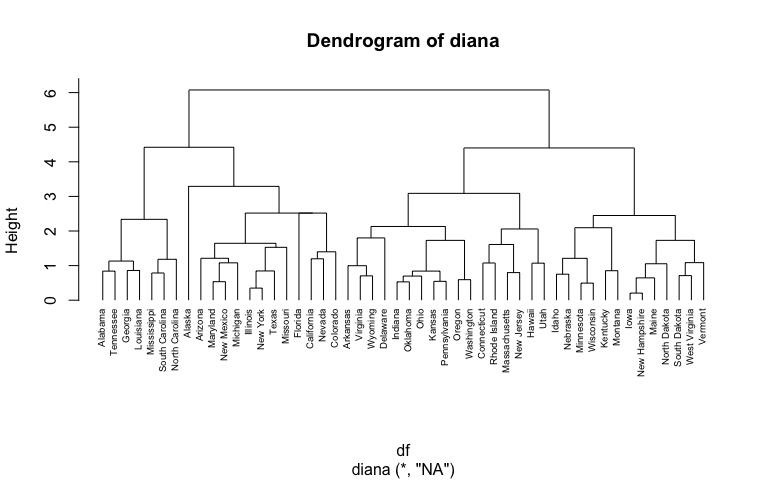
Hierarchical Cluster Analysis Uc Business Analytics R Programming Guide

A graph formally consists of a set of vertices V and a set of edges E between them.

Clustering coefficient of a tree. The clustering coefficient measures how connected a vertexs neighbors are to one another. The global clustering coefficient is defined as the number of closed triplets over the total number of triplets open and closed. Backward links may occur with this method.

Compute the clustering coefficient for nodes. Then at most k v k v -1 2 edges can exist between them this occurs when. Nodescontainer of nodes optional defaultall nodes in G Compute average clustering for.

By definition clustering coefficient of a node with degree is the ratio of the total number of existing edges between all its nearest neighbors and the number of all possible edges between them. The first based on the matching coefficient and the second based on the Jaccard index. One can distinguish between local measurements of the clustering of nodes in a graph and global measurements of the clustering coefficient of an entire graph.

A triplet which is connected with three edges is called a closed triplet. Y_hc hcfit_predict X In this case we need to provide the number of clusters as input here n_clusters 3. Compute the average clustering coefficient for the graph G.

The formula to compute the local clustering coefficient is as follows. The relationship between the cohort class and node clustering coefficient of trees was weak r 0018 P 0008. A triplet which is connected by two edges is called an open triplet.

The neighborhood for a vertex is defined as its immediately connected neighbors as follows. Im doing some research and Ive come to a point where I have calculate the clustering coefficient of a graph. To compute C n we use the number of triangles a node is a part of T n and the degree of the node d n.

Variant 1 Define the clustering coefficient c 1 as the probability that two incident edges are completed by a third one to form a. Silhouette Coefficient or silhouette score is a metric used to calculate the goodness of a clustering technique. The clustering coefficient of the whole network is the average of all individual.

The number of edges connecting a vertexs neighbors the total number of possible edges between the vertexs neighbors. More specifically it is calculated as. The clustering coefﬁcient C p is deﬁned as follows.

The local clustering coefficient C n of a node n describes the likelihood that the neighbours of n are also connected. The algorithm for hierarchical clustering Cutting the tree Maximum minimum and average clustering Validity of the clusters Clustering correlations. The coefficients of the distance equation are α i i α β αα γ k j j k i j n n n n 0.

The clustering coefficient for the graph is the average C 1 n v G c v where n is the number of nodes in G. Its value ranges from -1 to 1. Of the many dissimilarity coefficients that are possible to define between the samples.

The average clustering coefficient sum of all the local clustering coefficients divided by the number of nodes for the symmetric employee-network is 0867. In data mining and statistics hierarchical clustering also called hierarchical cluster analysis or HCA is a method of cluster analysis which seeks to build a hierarchy of clusters. A method of matrix analysis of group structure.

For unweighted graphs the clustering of a node u is the fraction of possible triangles through that node that exist c u 2 T u d e g u d e g u 1 where T u is the number of triangles through node u and d e g u is the degree of u. Strategies for hierarchical clustering generally fall into two types. We define as the number of vertices in the neighbourhood of a vertex.

T1 getTrace X y_hc 0 0 X y_hc 0 1 X y_hc 0 2 s 4 cred label 1. An edge connects vertex with vertex. This is a bottom-up approach.

The local clustering coefficient for a vertex is then given by the. So the clustering coefficient for our network has the following simple formula. Suppose that a vertex v has k v neighbours.

Although the clustering coefficient is often used there are actually two variants of it which may have completely different values. That is where is the number of nodes of the network. Spearmans rank correlations between tree cohort class and dbh 12 height node degree and node clustering coefficient and between tree node degree and clustering coefficient are shown independently for each plot in Table 1.

These are recognizable when the dendrogram no longer exhibits its simple tree-like structure in which each fusion results in a new cluster that is at a higher distance level moves from right to left. It was introduced in R. We can see the results of the clustering in a 3D graph with the following code.

Local clustering coefficient. Means clusters are well apart from each other and clearly distinguished. The Local Clustering Coefficient algorithm computes the local clustering coefficient for each node in the graph.

In the symmetric employee-network you will find that Michelle has a local clustering coefficient of 067 and Laura has a local clustering coefficient of 1. The local clustering coefficient is a ratio of the number of triangles centered at node i over the number of triples centered at node i. Clustering coefficient E-R networks CER p k N practically there is no clustering large random networks are tree-like networks k 2E N p N1 pN C G triangles connected triples.

In some sense it measures how close a node i and its neighbors are to being a complete graph.

Clustering Coefficient An Overview Sciencedirect Topics