Cluster Graph Theory

Desember 08, 2020 Posting Komentar

Clusters are believed to be an intermediate state between single atom and bulk system 12. Transform the data into a graph representation.

Clustering Graph An Overview Sciencedirect Topics

In this chapter we will look at different algorithms to perform within-graph clustering.

Cluster graph theory. The essential yet often neglected step in the cluster analysis is validation of the clustering results. Graph partitioning Each connected component is a cluster. This paper presents a novel cluster validity index which is the modification of the well-known Dunns index.

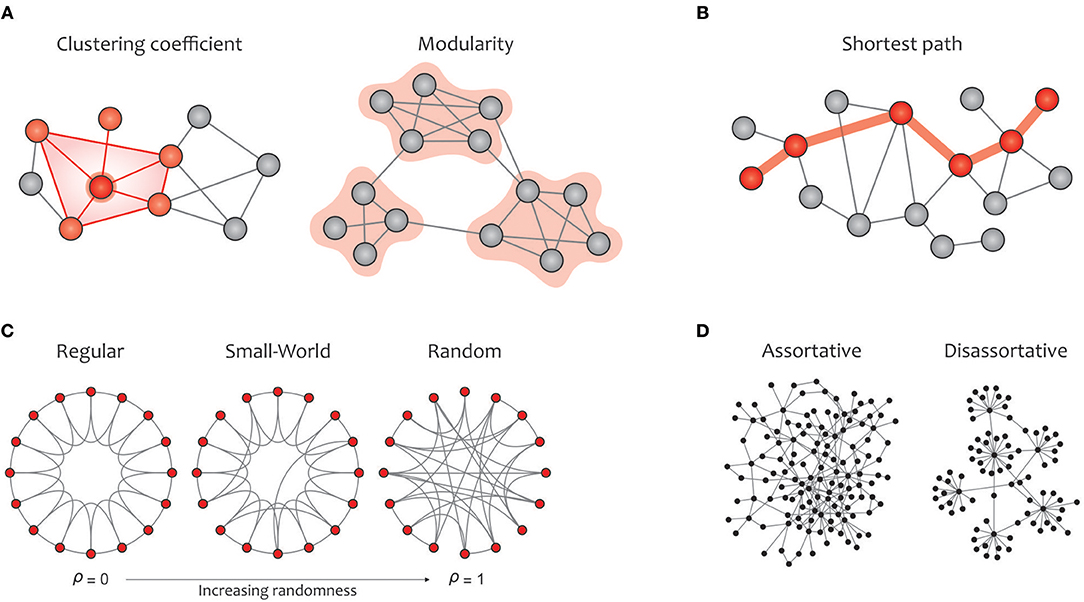
The algorithm is centralized where all calculations take place in a central point. Clustering as Graph Partitioning. In graph theory a clustering coefficient is a measure of the degree to which nodes in a graph tend to cluster together.

In Lianming et al 20 graph theory was utilized to detect boundary nodes and isolated nodes. A cluster analysis method based on graph theory was implemented in a computer program that can run on many operating systems and is available at the journals. In graph theory a clustering coefficient is a measure of the degree to which nodes in a graph tend to cluster together.

In statistical physics and mathematics percolation theory describes the behavior of a network when nodes or links are added. In Zhao et al 18 the author utilizes clustering graph theory property to convert network into small graphs to detect network holes. Numerical studies of Kleins graph-theoretic cluster expansion ansatz CEA are made for several thermochemical properties and graph-theoretic topologica indices of alkanes.

Clustering is one of the main tasks in unsupervised machine learning. The proposed algorithm was named BRGT. Vertices are the data points to be clustered Edges are weighted based on similarity between data points.

Clusters can be an ideal approach to understand how the atoms assemble to form nanomaterials. From this complete graph the minimum spanning tree of the graph. The graph by name connected graph incomplete graph non-simple graph closeness central ity clustering coefficient.

This clustering method is based on the most commonly used Euclidean distance from which a complete graph is then constructed. The ansatz expresses any molecular property in terms of unique numerical contributions arising from structural descriptors subgraphs of the molecular structural formula called clusters. The applications of percolation theory to materials science and in many other disciplines are discussed here and in the articles network theory.

Into a predetermined number of groups using the discrete mathematical tool graph theory. Evidence suggests that in most real-wor Clustering Coefficient in Graph Theory. The goal is to assign unlabeled data to groups where similar data points hopefully get assigned to the same group.

The data of a clustering problem can be represented as a graph where each element to be clustered is represented as a node and the distance between two elements is modeled by a certain weight on the edge linking the nodes 1. Within-graph Clustering Within-graph clustering methods divides the nodes of a graph into clusters Eg In a social networking graph these clusters could represent people with samesimilar hobbies 9 Note. The groups ranging from 2 to 10000 atoms are known as clusters.

This is a geometric type of phase transition since at a critical fraction of addition the network of small disconnected clusters merge into significantly larger connected so-called spanning cluster. Graph clustering is an important subject and deals with clustering with graphs. Sperner Grid a concept satisfies all such natures required wo uld be more.

The proposed method operates as follows. Graph Clustering is the process of grouping the nodes of the graph into clusters taking into account the edge structure of the graph in such a way that there are several edges within each cluster and very few between clusters. Thus in graph clustering elements within a cluster are connected to each other but have no connection to elements outside that cluster.

Graph Clustering intends to partition the nodes in the graph into disjoint groups. Variants using Spectral Clustering Spectral graph theory Spectral graph theory studies how the eigenvalues of the adjacency matrix of a graph which are purely algebraic quantities relate to combinatorial properties of the graph. Clustering for Graph Datasets via Gumbel Softmax.

Our proposal is based on its generalization considering the shortest paths between data points in the Gabriel graph. Spectral clustering studies the relaxed ratio sparsest cut through spectral graph theory. Spectral clustering is a technique with roots in graph theory where the approach is used to identify communities of nodes in a graph based on the edges.

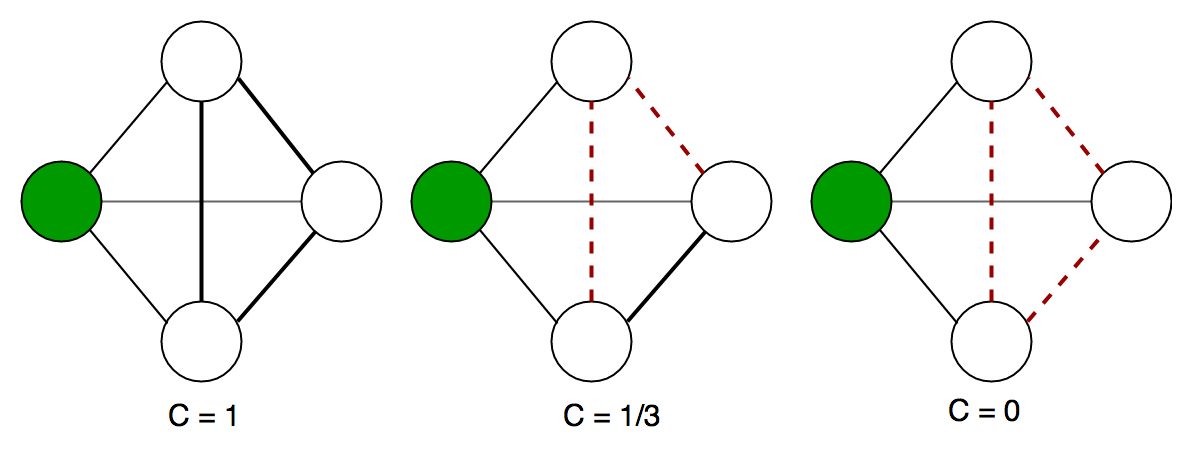
Clustering Coefficient In Graph Theory Geeksforgeeks